Berpikir Matematis dengan Metode Analogi

Belajar Daring - Pada artikel ini Admin akan membahas mengenai Berpikir Matematis dengan Metode Analogi.

Berasumsi atau berpikir tidak hanaya untuk memperoleh pengetahuan yang belum pernah didapat melainkan agar memperluas informasi (Prihanti, 2015).

Pengetahuan sebagai hasil pola berpikir yang telah dimiliki seseorang memungkinkanaya dengan sebuah keaadaan yang terjadi sehingga bisa mengatasi persoalan yang ada, dan memberi penyelesaiannya (Izhar, 2016).

Berpikir Analogi

Analogi dalam kamus bahasa Indonesia diartikan sebagai persamaan atau persesuaian antara dua hal yang berbeda.

Menurut Soekadijo (1999: 139) analogi adalah berbicara tentang dua hal yang berlainan, yang satu bukan yang lain, tetapi dua hal yang berbeda itu dibandingkan satu dengan yang lain.

Dalam analogi yang dicari adalah keserupaan dari dua hal yang berbeda, dan menarik kesimpulan atas dasar keserupaan itu.

Dengan demikian analogi dapat dimanfaatkan sebagai penjelas atau sebagai dasar penalaran.

Ada pun analogi secara mendalam, yaitu sebagai berikut:

Mampu belajar dan melakukan apa yang diinginkan secara mandiri,

Menerapkan teknik pemecahan masalah dalam berbagai bidang,

Mampu menstrukturkan masalah dengan teknik formal, seperti matematika, dan menggunakannya untuk memecahkan masalah,

Dapat mematahkan pendapat yang tidak relevan serta merumuskan intisari,

Terbiasa menanyakan sudut pandang orang lain untuk memahami asumsi serta implikasi dari sudut pandang tersebut,

Peka terhadap perbedaan.

Salah satu metode untuk bernalar adalah dengan menggunakan analogi.

Soekardijo (1999: 27) analogi adalah berbicara tentang suatu hal yang berlainan, dan dua hal yang berlainan lalu dibandingkan.

Selanjutnya, jika dalam perbandingan hanya diperhatikan persamaan saja tanpa melihat perbedaan, maka timbullah analogi.

Diane (Setyono, 1996: 3) mengatakan bahwa dengan analogi suatu permasalahan mudah dikenali, dianalisis hubungannya dengan permasalahan lain, dan permasalahan yang kompleks dapat disederhanakan.

Secara umum, Mundiri (2000: 26) mengemukakan bahwa terdapat 2 (dua) analogi yaitu sebagai berikut:

Analogi Deklaratif

Analogi deklaratif adalah analogi yang digunakan untuk menjelaskan sesuatu yang belum diketahui atau masih sama, dengan menggunakan hal yang sudah dikenal.

Contoh: Menjelaskan angka 16

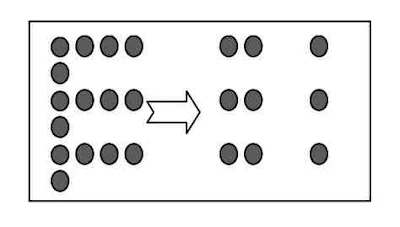Gambar 1

Analogi Induktif

Analogi induktif adalah analogi yang disusun berdasarkan persamaan prinsip dari dua hal yang berbeda, selanjutnya ditarik kesimpulan bahwa apa yang terdapat pada hal pertama terdapat pula hal yang kedua.

Contoh: Lihat pada Gambar 2

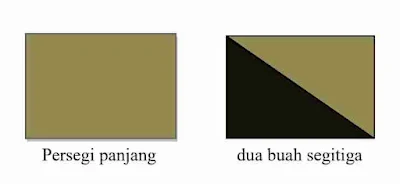Gambar 2

Pentingnya Analogi

Dengan proses atau aktivitas berpikir yang mengaitkan kesamaan antara pengetahuan yang sudah dimiliki dengan masalah yang dihadapi.

Pengetahuan yang sudah dimiliki in akan menjadi dasar pengembangan matematika dan pemecahan masalah yang ada. Kemampuan berpikir analogi ini akan mengantarkan ke penemuan berikutnya yang akan sangat bermanfaat bagi masa depan bangsa.

Benarnya pendapat Isoada dan Katagiri (2012:57) yang menyatakan bahwa: “Analogical thinking is an extremely important method of thinking for establishing perspectives and discovering solutions.”

Artinya, kemampuan berpikir analogi adalah sangat penting dalam membentuk perspektif dan menemukan pemecahan masalah.

Di samping itu, perhatikan pernyataan Kepler berikut berkait dengan pentingnya analogi ini: “And I cherish more than anything the analogies, my most trustworthy masters. They know all the secrets of Nature, and they ought to be the least neglected in Geometry.”

Pernyataan Kepler sebagaimana dikutip English (1999:22) di atas merupakan ungkapan tentang peran sangat penting dari analogi.

Kepler menyatakan bahwa ia menghargai analogi melebihi dari yang lainnya.

Dengan jujur Kepler mengakui bahwa analogi tersebut merupakan gurunya yang sangat ia percayai.

Sang guru (analogi), menurut Kepler, mengetahui segala hal tentang rahasia alam raya, dan analogi tersebut akan merupakan hal yang paling sedikit diabaikan di Geometri.

Judul tulisan English (1999:22) adalah: ‘Reasoning by Analogy’ atau ‘Penalaran dengan Analogi’.

English (1999:22) juga menyatakan bahwa selama peradaban manusia, analogi telah memainkan peran yang sangat penting di dalam pengembangan ilmu pengetahuan: “Throughout history, they have played a powerful role in advancing our knowledge of the world.”

Demikianlah penjelasan singkat pada artikel yang membahas mengenai Berpikir Matematis dengan Metode Analogi, semoga dapat bermanfaat.

Terima Kasih.

Selamat Belajar Daring.