Contoh Cara Berpikir Matematis (Sebuah Penalaran Analogis, Induktif, dan Deduktif)

Belajar Daring - Selamat datang di Blog Belajar Daring, pada materi Matematika kali ini Admin akan membagikan tentang Contoh Cara Berpikir Matematis (Sebuah Penalaran Analogis, Induktif, dan Deduktif).

Ada banyak contoh kasus disekitar kita yang berkaitan mengenai pengukuran dalam berbagai situasi seperti jual beli barang, suhu, kecepatan, waktu, dan lain-lain.

Misalnya, “keadaan yang memahami kebiasaan dan memprediksi masa depan bedasarkan data masa lalu dan data saat ini”, “Keadaan dimana sifat kejadian itu dan keadaan yang umum dengan mengulangi beberapa percobaan”, “keadaan dimana isi yang telah disimpulkan, kemudian dijelaskan kepada orang lain”.

Kemampuan seperti ini benar-benar harus dimiliki, karena kemampuan ini sangat diperlukan dalam kehidupan sehari-hari.

Khususnya, aritmatika dan matematika yang dianggap sebagai mata pelajaran yang cocok untuk memperoleh kemampuan menyimpulkan seperti itu.

Oleh karena itu, dalam artikel ini akan menyimpulkan 3 hal, yaitu “analogis”, “induktif”, dan “deduktif” mengenai kesempatan untuk mempersiapkan matematika Sekolah Menengah Pertama, bahkan dapat di sadari pada pembelajaran biasa, khususnya pentingnya pengajaran.

Penalaran Analogis

Contoh Penalaran Analogis

Penalaran analogis adalah cara berpikir bahwa masalah yang telah dipecahkan sebelumnya, dapat diselesaikan dengan metode yang sama kali ini.

Khususnya, dalam matematika Sekolah Dasar ada gagasan yang sering digunakan, seperti “Apakah mungkin menghitung pecahan dan desimal dengan cara yang sama dengan bilangan bulat?”.

Oleh karena itu, gagasan dalam artikel ini adalah “Terapkan aturan dan jenis yang ditemukan sebelumnya dan pikirkan dengan cara yang sama”

Cara Berpikir Matematis dengan Penalaran Analogis

Contoh Penalaran Analogis

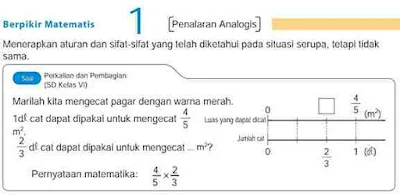
Cara berpikir matematis 1 merupakan contoh “Penalaran analogis”.

Saat mempertimbangkan perhitungan “pecahan × pecahan”, pengali dan penyebut pengali dikalikan, diubah menjadi bilangan bulat dan akhirnya dikembalikan ke pecahan untuk mendapatkan jawabannya.

Pada saat itu “aturan yang ditemukan sebelumnya” adalah gagasan untuk mengibahnya menjadi bilangan bulat dengan “desimal × desimal”.

Hal tersebut sudah berlaku untuk desimal, mungkin dapat berlaku juga untuk pecahan.

Penalaran analogis ini digunakan dalam situasi seperti pengenalan pengurangan.

Pengurangan di Sekolah Dasar sebagai penghitungan kembali operasi penjumlahan, jadi ini dapat digunakan dalam situasi mengingat bilangan negatif dimasukkan.

Hal tersebut dapat dipertimbangkan dengan cara yang sama.

Penalaran Induktif

Contoh Penalaran Induktif

Penalaran induktif biasanya dikatakan sebagai cara berpikir yang digunakan dalam sains.

Mengulangi percobaan, mempertimbangkan hasil tersebut, dan menduga hal seperti yang diharapkan terjadi.

Gagasannya adalah untuk mengetahui aturan dan ide umum dengan memeriksa banyak data.

Dalam matematika, ini sering digunakan dalam situasi mencari sifat bilangan bulat, seperti “Memprediksi apakah jumlah bilangan genap dan ganjil akan menjadi ganjil”.

Oleh karena itu, artikel ini memiliki gagasan “Memikirkan aturan dan sifat umum melalui beberapa hal konkret”.

Cara Berpikir Matematis dengan Penalaran Induktif

Contoh Penalaran Induktif

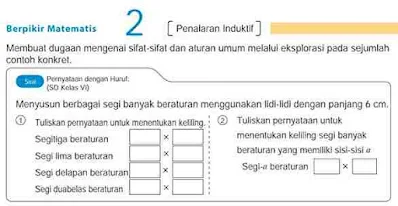
Cara berpikir matematis 2 adalah contoh Penalaran induktif.

Saat mempertimbangkan rumus untuk menghitung panjang keliling segi banyak beraturan, keteraturan ditemukan dengan menambah jumlah sisi secara bertahap seperti segitiga beraturan, segi lima beraturan, dan seterusnya.

Dengan demikian, rumus untuk menghitung panjang disekitar persegi adalah “panjang 1 sisi x α”.

Penalaran induktif ini adalah untuk menggambar beberapa lingkaran yang melewati titik-titik ujung garis, berpusat pada titik-titik pada garis berat vertikal garis bola, sehingga titik-titik pada garis-garis vertikal memiliki jarak yang sama dari kedua ujung garis.

Penalaran Deduktif

Contoh Penalaran Deduktif

Penalaran deduktif adalah cara berpikir yang muncul dalam bentuk “pembuktian”, yang dianggap sebagai hal penting dalam matematika Sekolah Menengah Pertama, misalnya, “Menggunakan definisi dan sifat yang telah terbukti untuk menemukan sifat baru dan menjelaskan bahwa sifat itu benar”.

Oleh karena itu, pada artikel ini, gagasannya adalah “Memikirkan tentang alasan berdasarkan aturan dan sifat umum yang ditemukan sebelumnya”.

Cara Berpikir Matematis dengan Penalaran Deduktif

Contoh Penalaran Deduktif

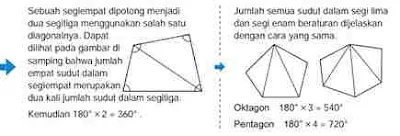
Cara berpikir matematis 3 adalah contoh dari Penalaran deduktif.

Alasan jumlah ukuran keempat sudut segi empat adalah 360° didasarkan pada fakta bahwa “jumlah sudut dalam segitiga adalah 180°” dan “segi empat dapat dibagi menjadi dua segitiga secara diagonal”.

Menemukan jumlah dari sudut dalam segi empat dan jumlah sudut bagian dalam dari segi banyak (poligon) lainnya.

Cara berpikir ini digunakan dalam situasi yang menjelaskan bahwa metode menggambar untuk memulihkan lingkaran dengan hanya satu bagian, benar berdasarkan sifat dari garis-garis vertikal.

Selanjutnya, selain menemukan istilah seperti “Penalaran analogis”, “Penalaran induktif” dan “Penalaran deduktif”, dengan mengetahui 3 penalaran tersebut dan bertujuan sebagai pembelajaran untuk diri sendiri, jadi tidak begitu penting untuk harus mengigat istilah ini.

Demikianlah artikel yang dapat Admin bagikan mengenai Contoh Cara Berpikir Matematis (Sebuah Penalaran Analogis, Induktif, dan Deduktif), semoga dapat bermanfaat.

Terima Kasih.

Selamat Belajar Daring.