Takakazu Seki (Sekitar Tahun 1640 - 1708)

Belajar Daring - Pada kesempatan kali ini Admin akan membagikan sebuah informasi mengenai seorang tokoh matematika yang bernama Takakazu Seki (Sekitar Tahun 1640 - 1708) yang berasal dari negara Jepang.

Takakazu Seki adalah seorang matematikawan Jepang yang menemukan pengembangan sistem notasi simbolis Jepang menggunakan batang penghitungan papan dengan mengindeks variabel yang tidak diketahui dan menghitung nilai pi ke dalam jumlah digit terpanjang selama era itu.

Takakazu Seki dihormati oleh banyak matematikawan Jepang di luar sekolahnya setelah kematiannya.

Biografi Takakazu Seki/ Seki Kowa

Source: commons.wikimedia.org

Informasi Pribadi:
Lahir: Maret , 1642 Edo atau Fujioka, Jepang
Meninggal: 5 Desember 1708 (kalender Gregorian) Jepang
Kebangsaan: Jepang
Bidang: Matematika

Seki Kowa lahir pada bulan Maret 1642 di Edo atau Fujioka, Jepang.

Dia lahir dari Klan Uchiyama, subjek Ko-shu han, dan diadopsi ke dalam keluarga Seki, subjek dari Shogun.

Terdapat berbagai teori tentang tahun kelahiran dan tempat lahir dari Seki Takakazu yang hingga kini masih belum jelas.

Berdasarkan beberapa penelitian, terdapat teori yang menyatakan bahwa ia lahir pada tahun 1637, ada yang menyebutkan ia lahir tahun 1642 di Joshu Fujioka (yang sekarang adalah kota Fujioka, perfektur Gunma), ada pula yang menyatakan bahwa ia lahir di Edo (sekarang Tokyo).

Meskipun ia adalah sosok hebat dalam sejarah perkembangan matematika di Jepang, kesimpangsiuran teori-teori tersebut konon disebabkan karena terputusnya keluarga Seki sehingga sejarah tentangnya masih belum banyak diketahui hingga sekarang.

Sementara di Ko-shu han, dia terlibat dalam sebuah proyek survei untuk menghasilkan peta yang dapat digunakan untuk tanah majikannya.

Dia menghabiskan waktu bertahun-tahun dalam mempelajari kalender Cina abad ke-13 untuk memperbaiki kekurangakuratan yang digunakan di Jepang pada waktu itu.

Seki Kowa atau Seki Takakazu adalah seorang matematikawan dari Jepang zaman Edo yang menciptakan sistem notasi baru matematika yang digunakan dibanyak teorema dan teori.

Sumbangan terkenal dari Seki pada aljabar adalah menemukan Determinan.

Beliau hanya dapat menyelesaikan matrik ordo 2x2 dan 3x3, dan gagal untuk ordo yang lebih tinggi.

Akan tetapi muridnya yaitu Laplace berhasil menyelesaikan unsur untuk matriks ordo yang lebih tinggi yang digunakan untuk mengeliminasi variabel pada sistem persamaan.

Seki Takakazu adalah ahli wasan (matematika Jepang) yang aktif di zaman Edo, yang sekarang disebut “sekisei”.

Seki meletakkan dasar bagi perkembangan selanjutnya dari matematika Jepang yang dikenal sebagai wasan.

Metode Penulisan Samping

Diantara banyak hal yang tersisa dari pencapaian Seki Takakazu, dan salah satu yang paling terkenal adalah gagasan ekspresi aljabar yang disebut “metode penulisan samping”.

Operasi dasar dari “metode penulisan samping” ditunjukkan pada gambar tabel di bawah ini:

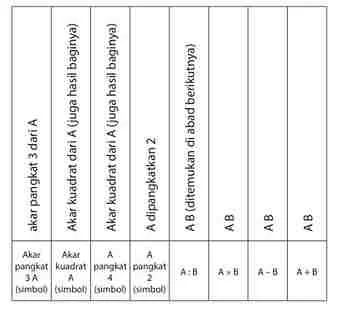Metode penulisan samping

Karena wasan biasanya ditulis secara vertikal, maka metode tersebut berbeda dari ekspresi lainnya pada saat itu.

Seki Takakazu telah memiliki banyak pencapaian selain “metode penulisan samping”, di antaranya menemukan rasio keliling yang benar hingga 11 digit dan menemukan deter-minannya.

Determinan

Seki Kowa mempublikasikan konsep determinan pertama kali di Jepang tahun 1683. Seki menulis buku Method of Solving the Dissimulated Problems yang memuat metode matriks.

Akan tetapi Seki Kowa belum menggunakan istilah determinan dalam memaparkan konsep determinan ini.

Walaupun Seki Kowa telah memperkenalkan bentuk determinan dan memberi metode umum untuk menghitungnya.

Seki Kowa menemukan determinan khusus untuk matriks ordo 2 x 2, 3 x 3 , 4 x 4, 5 x 5 saja.

Setelah itu diikuti Leibniz dalam suratnya ke 1’Hopital tahun 1683 di Eropa menjelaskan sistem persamaan misalnya:

10+11x+12y=0

20+21x+22y=0

30+31x+32y=0

Hanya memiliki satu penyelesaian karena 10.20.32+11.22.30+12.20.31=10.22.31+11.20.32+12.21.30 yang tidak lain merupakan syarat determinan koefisien sama dengan nol.

Tetapi Leibniz sesungguhnya tidak bermaksud menggunakan bilangan, ada pun yang dinyatakan dengan 21 adalah a21.

Leibniz menggunakan istilah resultant untuk kombinasi hasil kali koefisien dari determinan tersebut.

Seiring bergulirnya waktu Maclurin menulis Treatise of Algebra pada tahun 1730 dan baru diterbitkan tahun 1748.

Source: commons.wikimedia.org

Buku memuat pembuktian Aturan Cramer untuk matriks 2 x 2 dan 3 x 3.

Selajutnya konsep determinan diperjelas oleh Cramer pada tahun 1750 dalam buku Introduction to the Analysis of Algebraic Curve memberikan aturan umum untuk aturan Cramer pada matriks n x n tetapi tidak ada bukti yang diberikan.

Tahun 1764, Bezout memberikan sebuah metode menghitung determinan, begitu juga Vandermonde pada tahun 1771.

Dan tidak kalah pentingnya tahun 1722, Laplace menggambarkan aturan ekspansi Laprace dan ia menamakan determinan dengan resultant.

Istilah determinan pertama kali digunakan oleh Gauss dalam Disquistiones Arithmeticae (1801).

Dalam buku tersebut terdapat dalam pembahasan bentuk-bentuk kuadrat dengan menggunakan determinan.

Cauchy pada tahun 1812 memaparkan istilah Eliminasi Gauss, yang telah digunakan di Cina tahun 200 SM dimana orang pertama menggunakan istilah determinant dalam konteks modern.

Karya-karya Cauchy hampir mewakili konsep determinan modern.

Dia merintis konsep ‘minor’ dan ‘adjoints’, serta hasil kali matriks.

Dalam karya tahun 1841 ia menggunakan tanda dua garis vertikal untuk menunjukkan determinan.

Saat ini konsep Cauchy dapat dinyatakan sbagai berikut.

Determinan dengan Minor dan kofaktor

Kofaktor dan minor hanya berbeda tanda Cij=±Mij untuk membedakan apakah kofaktor pada i.

det(A3x3)

= a11(a22a33 - a23a32) - a12(a21a33 - a23a31) + a13(a21a32 - a22a31)

= a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32

Perhitungan Pi

Kontribusi Seki yang lainnya adalah pembetulan dari lingkaran, yaitu, perhitungan pi.

Ia memperoleh nilai π yang benar ke tempat desimal 10, menggunakan apa yang sekarang disebut proses delta-squared Aitken, ditemukan kembali pada abad ke-20 oleh Alexander Aitken.

Demikianlah informasi tokoh matematika dari Jepang yaitu Takakazu Seki (Sekitar Tahun 1640 - 1708)yang dapat Admin bagikan kali ini, semoga artikel ini dapat bermanfaat.

Terima Kasih.

Selamat Belajar Daring.